概述:本文主要讲述了图神经网络的工作原理以及基础知识。
图神经网络
图神经网络优势
- 增加了图的结构信息
基础理论
图神经网络的输入主要分为两部分:
- 图结构 G = (V,E)
- 节点特征
消息传递
图神经网络的消息传递包含的两部分:
- 相邻接点之间的信息交换
- 更新网络节点
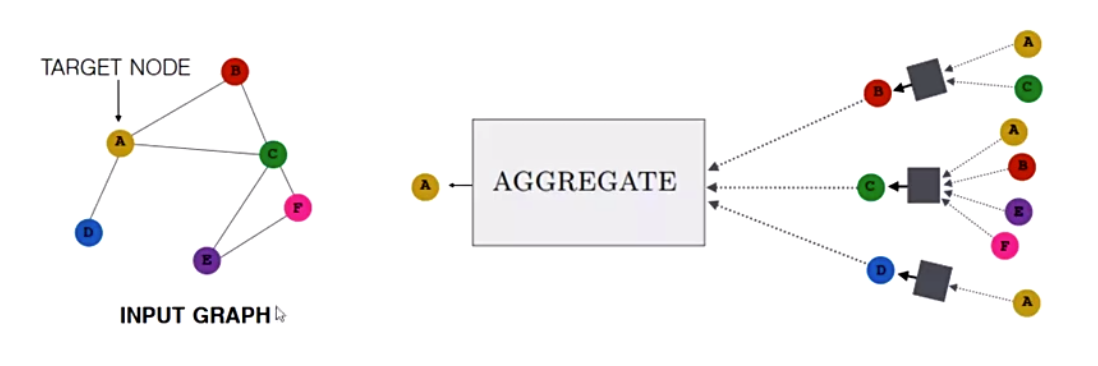
上图是图神经网络信息传递的一个实例,上图为节点A使用双层图神经网络进行消息传递时的方式,首先找到A节点的相邻节点,然后再找到相邻接点的相邻接点,A的相邻接点使用Aggregate函数合并全部其相邻节点的信息,更新到相邻接点,然后A节点再使用Aggregate函数合并更新后的节点信息到自身,完成消息传递与节点信息的更新。使用
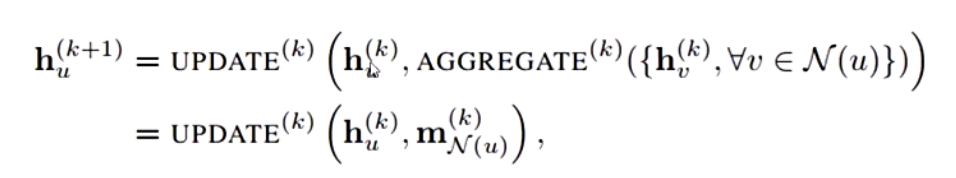
其中h表示节点的表示向量,$h{u}^{k}$即表示节点u在第k层的表示向量,N(u)表示v的全部邻域节点,在公式中我们可以看出进行u节点第K+1层向量的更新,需要节点u在第k层的向量表示$h{u}^{k+1}$之外,还需要与u相邻的前全部邻域节点在第k层上的表示Aggregate后的结果。
不同的GNN之间的不同点主要在于UPDATE函数不同、聚合函数不同、消息传递不同。
Basic GNN
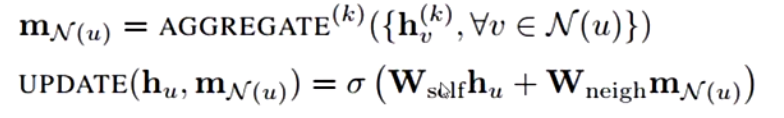
在Basic GNN中,UPDATE函数使用节点u在k层的神经网络进行线性变换与节点u的邻域信息线性变化相加,再进行sigmod线性变换的方式进行。
Self-Loop GNN
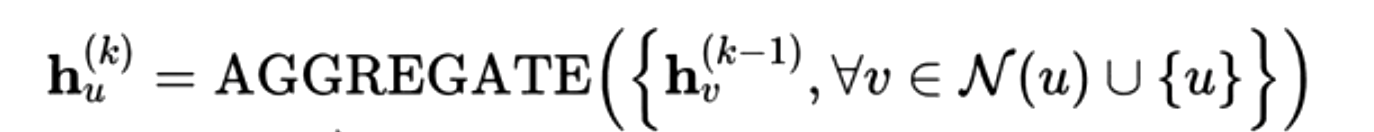
在学术界使用的更多的图神经网络为Self-Loop GNN,在上面的Self-Loop公式中可以看出,Aggregate聚合函数聚合的不止包含节点u的邻域向量表达,还包含了节点u自身的向量表示,因此也就不再需要UPDATE函数来进行节点节点信息的更新。其矩阵形式为:
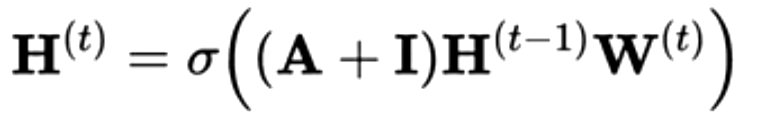
其中A为图数据的邻接矩阵,I为单位矩阵,此处+即为Aggregate的实现,即每个节点增加了一个自循环,乘以上一层的数据表示$H^{t-1}$,和可更新的参数矩阵W,然后经过Sigmod进行处理,即得到更新。
这里我们可以看出,在Self-Loop GNN中将邻域节点的参数矩阵和自身的参数矩阵进行了合并,因此表达能力将会有所下降
聚合操作(Aggregate)
基础聚合操作的种类
Sum
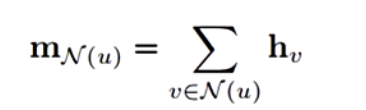
存在问题;难以进行参数更新
有些节点的邻居可能非常多,相加导致向量表示的数值非常大,而有些节点的邻居非常少,相加的向量表示的数值非常小,两者的差距很大,导致图神经网络很难进行更新,
Mean
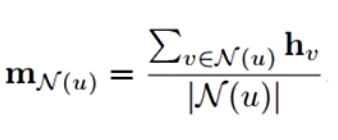
为了解决Sun聚合函数由于节点间可能由于节点邻居节点数量不等造成的图神经网络难以进行更新的问题,引入了节点的度(邻居的数量)来对向量累加和做归一化,
Symmetric normalization
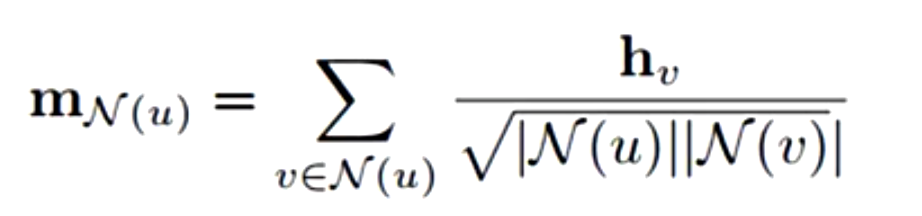
在GCNN论文中论文中,认为对于节点分类的任务中,图数据中度很大的节点可能并不是很重要的论文,因此不止使用自身的度做归一化,还加入了邻居节点的度做归一化,从而减弱被具有大量邻居节点的对该节点的影响。
不同聚合方式的选用
- 对于需要使用学到的embedding向量去区分不同节点的度的情况,只能使用sum
- normalization的方式将损耗一定的图结构信息
为什么论文中大多还是采用对称标准化的聚合操作?
这是因为在大多数的场景下,节点本身的特征远远比节点间的结构信息更重要,而使用Symmetric normalization能够降低节点间结构信息的影响,因此更多的论文更愿意选用Mean和Symmetric normalization。
Neighborhood Attention
Neighborhood Attention是一种更加复杂的Aggregate方式,它在进行邻域信息整合时将给与每个节点一个attention权重,让网络来自动进行分配。下面公式中$α_{u,v}$即为节点u分配给其各个相邻节点v的权重值。
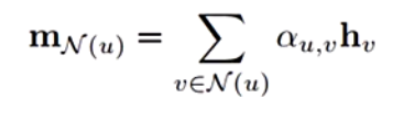
下面是几种常见的neighborhood attention的具体实现,其主要区别在于$h_u、h_v$之间如何由计算其attention系数:
GAT-style attention
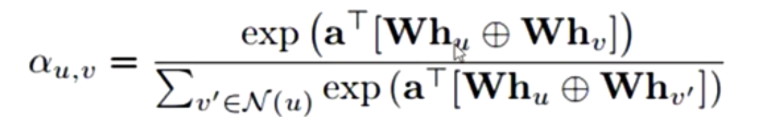
节点u、相邻的节点v对其自身的向量表示用可更新的参数矩阵W做线性变换,然后将二者进行拼接,然后乘以可学习的参数a,然后使用softmax函数将其值归约到0~1之间。
bliinear attention
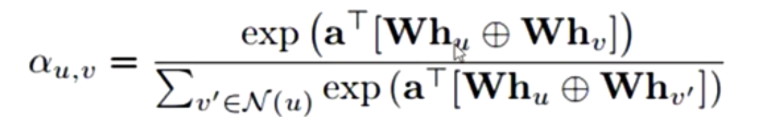
MLP attention
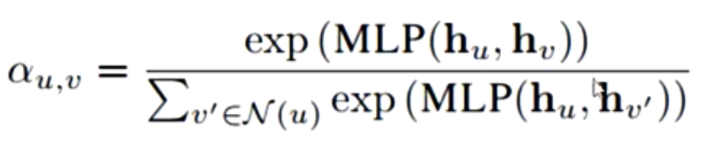
更新操作(Update)
Over-Smoothing
在图图神经网络的训练过程中,常常会出现随着训练轮数的增加,造成全部节点的表示都变得十分相似的问题,在JKNET论文中从理论上证明了GNN中节点之间的影响力和节点上随机游走的停滞概率成正比:
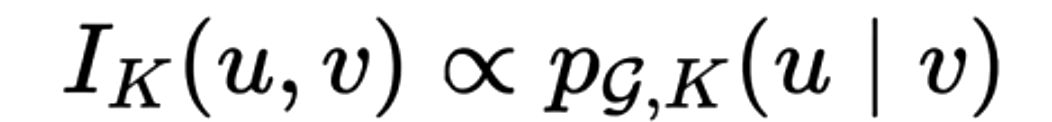
$I_K^{(u,v)}$代表v对于u的影响力,$p_k{(u|v)}$表示从出发进行K步随机游走的概率。而随机游走具有最终将停留到稳态分布的性质,稳态分布代表图上所有的节点到图上其他节点的概率都是相同的,因此当K很大时,图神经网络将无法捕捉局部结构信息。最终导致当图神经网络在进行层数加深时,效果将出现显著的下降。这就需要采用特殊设计的Update函数来减缓这种情况的发生。
与深层神经网络中的残差结构的作用相类似
基础更新操作
concentration(拼接)
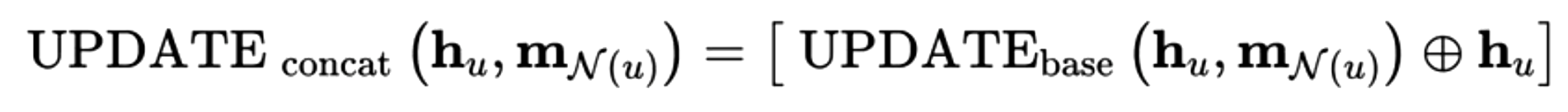
其中,$UPDATE_{base}$表示Basic GNN中基础的UPDATE更新函数,concentration UPDATE为基础更新函数与u节点本身的向量化表示的拼接,从而放大节点本身的特征。
Linear interpolation(线性加权)

其中,$α_1+α_2=1$,两者也都是可以自动进行更新的参数。从而保证了保留一部分节点本身的信息,让over-smoothing的速度变慢。
上面的两种UPDATE优化方式主要适用于
Gated Update
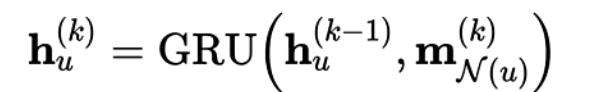
即使用RNN的方式来进行更新,上面的公式中即使用了GRU来进行更新。这种更新方式更适合一些复杂的推理任务,例如应用程序分析和组合优化问题。
RGCN
我们可以发现上面讨论的神经网络,全部都使用了全都只是用了节点特征和节点间的连接关系,但是并不能对连接关系的不同种类、关系特征进行表达,而RGCN正式为了将不同种关系同时在图神经网络中进行表达所设计的网络。
表达不同关系类型
首先,要介绍如何能够表达不同关系类型的RGCN网络,其主要的不同点在于聚合函数为:
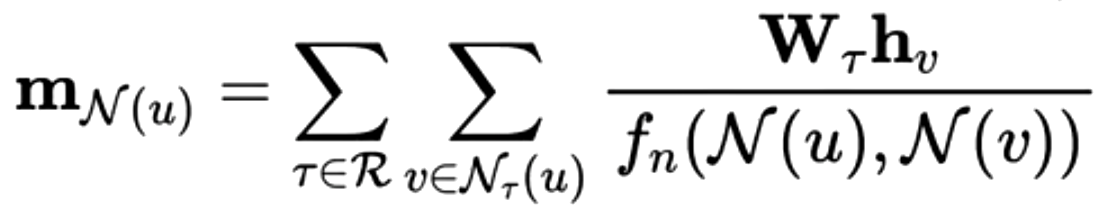
其中,R代表了全部关系的集合,而在RGCN中与一般图神经网络Symmetric normalization所不同的点在于对每个关系的类型都对单独训练一个权重矩阵,然后用这个权重来节点进行非线性变化,然后进行聚合。
这种方式存在的问题在于,如果关系的类型非常多的话,为每中类型的关系单独训练一个权重矩阵那么参数来那个将会变得非常巨大。
改进方式:
将每种关系类型训练一个权重矩阵该改为训练固定b个权重矩阵B,然后各种关系类型的权重矩阵都由各个权重矩阵进行加权组合得到,从而有效防止关系类型所产生的的参数数量过大的问题。

表达关系上的特征
要进行关系上特征的表达,只需将基础的聚合函数聚合节点信息更改为聚合节点信息与边特征表达拼接后的向量,这样进行聚合时得到的邻域信息中就既包含了节点上的信息也包含了边上的信息了。
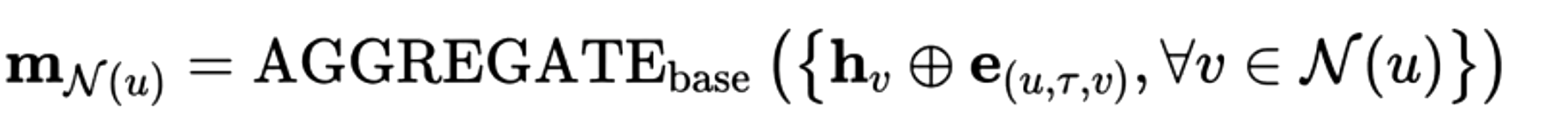
图神经网络任务类型
- 节点分类
- 图分类
- 关系预测