0%

强化学习5——PolicyGradient

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 3.2k 阅读时长 ≈ 3 分钟

概述：强化学习中除了前面讲解的Qlearning、DQN等Value-Base算法以外，还存在着一种Policy Gradient，本文将对其原理与实现过程进行讲解。

Policy-Base RL

  在前面的学习中，我们已经学习了很多种强化学习算法，这些强化学习算法无一例外，都在采用Value-Base的RL，即每一步都会有一个对应的Q值和V值(观测值)，而我们整个学习过程就是要计算出处于各个V对应的Q值，但是这个Q与V值的计算并不是我们的最终目标啊，那我们可以有什么办法不需要计算Q值吗？答案就是另一种RL算法：基于Policy-Base的RL，即直接根据策略是否能够达到最终目标而进行学习的强化学习算法。

核心思路：根据一个策略中是否能够达到最终目标作为奖惩，反向传递到整个策略中的各个行为对各个行为被选择的可能性进行更新。

优势：

  • 连续动作空间与高维动作空间中更加高效
  • 可以实现随机化策略
  • 在某种环境下，价值函数可能比较难以计算，而策略函数比较容易计算

缺点：

  • 通常容易收敛到局部最优而非全局最优
  • 由于每个epsoide结束才能进行更新，因此效率较低

Policy Gradient

  Policy-Base RL中最基础、最典型的算法就是Policy Gradient，该算法是尽管存在着效率低、难收敛等不足，虽是Policy的基础工作，但为后续Policy-Base RL与Policy-Base、Value-Base融合RL算法打下了基础。

1. 基本情况

  • 本质：蒙特卡洛算法+神经网络

  • 策略评价算法：蒙特卡洛算法

  • 损失函数：引入策略评价系数（蒙特卡洛算法中的G值）的交叉熵损失函数

  • 更新频率：回合制
  • 特点：
    • 直接输出action，不计算value，在连续区间内进行动作的选择
    • 回合制更新
    • 以神经网络预测概率值进行action随机选择：不再使用$\epsilon$-greedy算法进行行为选择，而是直接使用神经网络预测各个行为选择的预测值，然后根据这个概率进行行为随机选择
    • transition序列有序存储

【蒙特卡洛算法】

  从某个state出发，然后一直走，直到最终状态。然后我们从最终状态原路返回，对每个状态评估G值。所以G值能够表示在策略下，智能体选择路径的好坏。

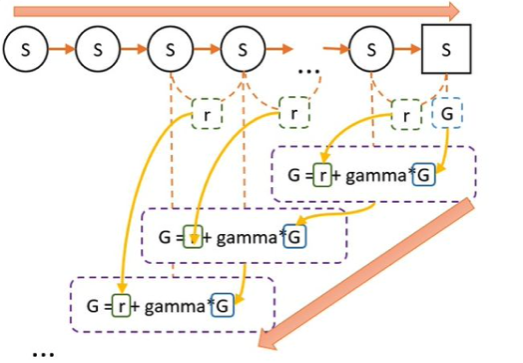
  在一次episode中，到达结束状态，我们计算蒙特卡洛方法中的所有G值。蒙特卡洛方法中，G值的计算方式为：

  1. 根据策略不断根据当前状态进行行为选择，并记录每一步选择获取的奖励r,直到完成任务。

  2. 完成任务后，从任务完成的状态开始向前回溯，计算每一个状态的G值。计算公式为

  最后一个状态的获得的总奖励值即为最后一个状态的G值。

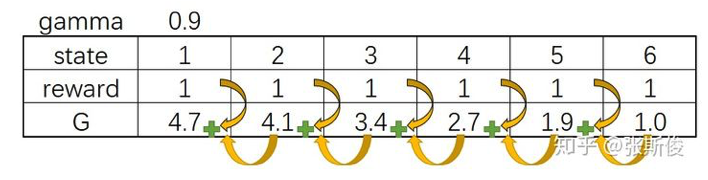
image

 在下面的实例中，假设我们在一个episode中，经过6个state到达最终状态，G值的计算如下所示。

image

2. 直观理解

  我们的Policy Gradient正需要一种算法可以做到，如果智能体选择了正确的决策，就让智能体拥有更多的概率被选择，如果智能体选择的行为是错的，那么智能体在当前转状态西选择这个行为的概率就会减少，由于蒙特卡洛方法中的G值可以直观衡量在策略表示下，智能体选择当前路径的好坏，因此将蒙特卡洛方法中的G值作为融入梯度更新算法中，如果到达当前节点的G值越大，那么这个节点的更新速率将越快。

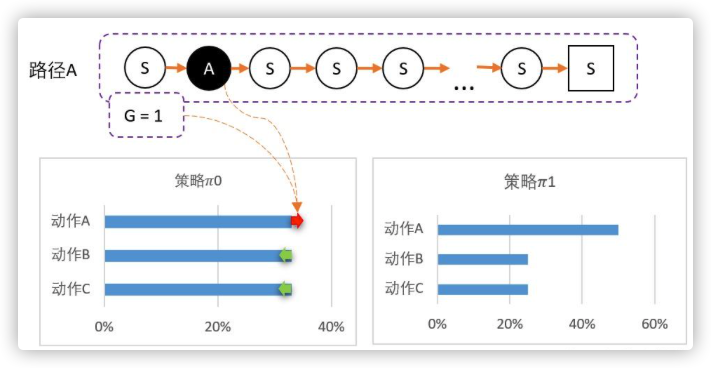
  例如假设从某个state出发，可以采取三个动作，当前智能体对这一无所知，那么，可能采取平均策略 0 = [33%,33%,33%]。第一步随机选择了动作A，到达最终状态后开始回溯，计算得到第一步的状态对应的 G = 1。

image

  我们可以更新策略，因为该路径选择了A而产生的，并获得G = 1；因此我们要更新策略：让A的概率提升，相对地，BC的概率就会降低。 计算得新策略为： 1 = [50%,25%,25%]

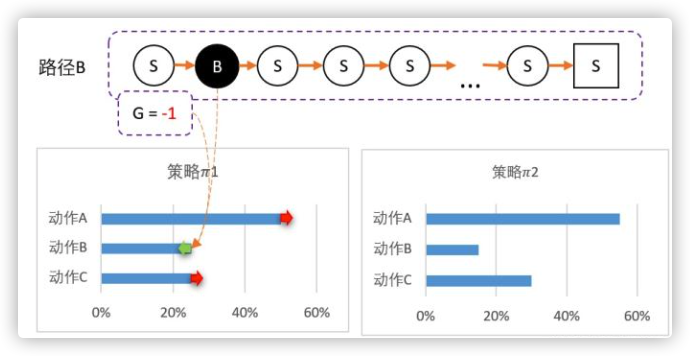
  虽然B概率比较低，但仍然有可能被选中。第二轮刚好选中B。智能体选择了B，到达最终状态后回溯，计算得到 G = -1。

image

  所以我们对B动作的评价比较低，并且希望以后会少点选择B，因此我们要降低B选择的概率，而相对地，AC的选择将会提高。计算得新策略为： 2 = [55%,15%,30%]

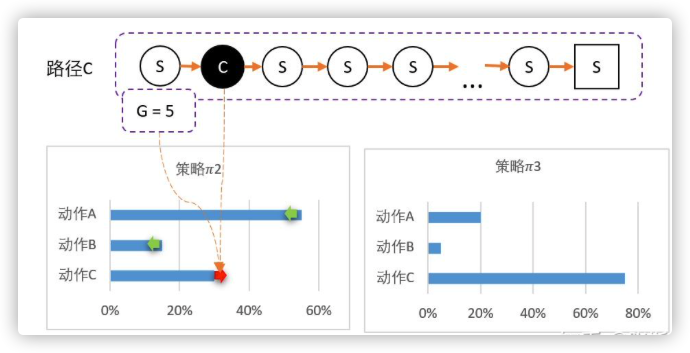
  最后随机到C，回溯计算后，计算得G = 5。

image

  C比A还要多得多。因此这一次更新，C的概率需要大幅提升，相对地，AB概率降低。 3 = [20%,5%,75%]

3.代码分析

更新框架

  Policy Gradient的更新策略与前面学习到的强化学习算法的基本框架类似,具体环节包括：

  1. 开始游戏，重置state
  2. 根据当前state选择action
  3. 与环境进行交互，获得obvervation_、reward、done、info
  4. 记录数据（这里的记录数据与DQN中的记忆库中存储不同，这里并没有记忆库）
  5. 计算G值，开始学习

  对应的代码如下:

1
2
3
4
5
6
7
8
for i_episode in range(num_episodes):    #1
            observation = env.reset()
            while True:
                action = RL.choose_action(observation)   #2
                observation_, reward, done, info = env.step(action)  #3
                RL.store_transition(observation, action, reward)  #4
                if done:
                    vt = RL.learn()    #5

  这里需要的主要有两点：

  1. 在第4步中的存储数据与DQN中不同，DQN中的数据存储将(s,a,r,s_,d)五要素存储在记忆体中，并在需要的时候在队列中随机进行抽取。而在Policy Gradient中，数据存储只需要记录(s,a,r)三要素即可，而且记录的顺序一定不能打乱，因为G值的计算与这些记录的顺序有关，需要从后往前进行回溯。
  2. Policy Gradient是回合制更新，而不是每步更新，这里我们可以从第5步中看出。而DQN则为每步更新算法。

行为选择

  在Policy Gradient算法中不再是使用$\epsilon$-greedy算法来进行，而是使使用神经网络预测出选择各个行为的概率值，然后按照这个概率值进行随机选择。具体的步骤如下：

  1. 根据观察值输入到网络中获取各个行为被选择的概率值
  2. 根据各个行为被选择的概率值，进行随机选择行为

  实现的代码为：

1
2
3
4
5
6
7
8
9
def choose_action(self, observation):
    observation = torch.FloatTensor(observation).to(device)
    network_output = self.network.forward(observation)
    with torch.no_grad():
        prob_weights = F.softmax(network_output, dim=0).cuda(1).data.cpu().numpy()   # 1
    
    action = np.random.choice(range(prob_weights.shape[0]),                          # 2
                              p=prob_weights)  # select action w.r.t the actions prob
    return action

状态存储

  Policy Gradient的记忆存储是将整个episode中的各个状态、行为、奖励三者进行有序存储，分别从存储在三个有序列表中。

1
2
3
4
5
6
7
# 将状态，动作，奖励这一个transition保存到三个列表中
self.ep_obs, self.ep_as, self.ep_rs = [], [], []

def store_transition(self, s, a, r):
  self.ep_obs.append(s)
  self.ep_as.append(a)
  self.ep_rs.append(r)

G值计算

   代码实现的思路如下：

  1. 创建全0向量，其大小与存储整个eposode中的reward的列表相同
  2. 反向循环计算G的值。
  3. 对G值进行归一化（可选，但是一般都需要，使用效果就更好）

  具体代码实现如下所示,其中：

1
2
3
4
5
6
7
8
9
10
def _discount_and_norm_rewards(self):
  discounted_ep_rs = np.zeros_like(self.ep_rs)    #1
  running_add = 0                                 #2
    for t in reversed (range(0, len(self.ep_rs))):
        running_add = running_add * GAMMA + self.ep_rs[t]
        discounted_ep_rs[t] = running_add
       
    discounted_ep_rs -= np.mean(discounted_ep_rs)   #3
    discounted_ep_rs /= np.std(discounted_ep_rs)  
    return discounted_ep_rs

带权重的梯度下降

  在Policy Gradient中的梯度下降与其他模型的梯度下降相比略有不同，因为他的损失函数是在交叉熵损失函数的基础上又加入了各个状态的G值作为权重系数，然后加权计算loss。

  1. 通过网络求得整个episode中各个obversation对应的action预测值分布。
  2. 和真实值action进行比较，求交叉熵损失neg_log_prob
  3. 将交叉熵损失net_log_prob与G对应相乘，获得带权重的loss
  4. 反向传播进行参数更新

具体代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def learn(self):
		# 求G值             
    discount_and_norm_rewards = torch.FloatTensor(self._discount_and_norm_rewards())

    softmax_input = self.network(torch.FloatTensor(self.ep_obs))  #1
    neg_log_prob = F.cross_entropy(input=softmax_input,target=torch.LongTensor(self.ep_as).to(device),reduction='none')                                                      # 2
    loss = torch.mean(neg_log_prob * discount_and_norm_rewards)   # 3

    self.optimizer.zero_grad()                                    # 4
    loss.backward()
    self.optimizer.step()

    # 每次学习完后清空数组
    self.ep_obs, self.ep_as, self.ep_rs = [], [], []

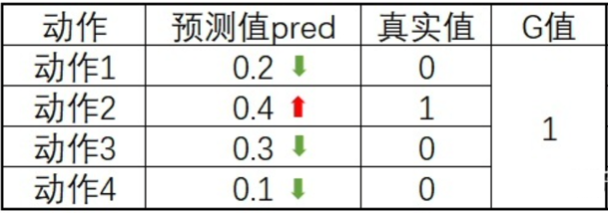
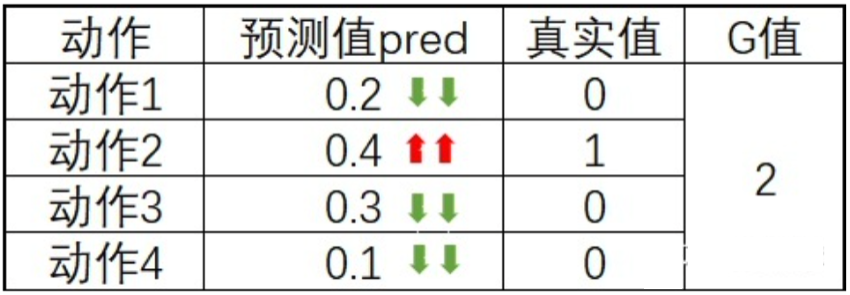
  这里我们以某一个状态为例对实际的意义进行讲解，在某个状态下，网络的预测值（logits）、真实值（ep_as）、G值（discounted_ep_rs_norm）可能存在下面的表情况，

image

image

  跟我我们对神经网络训练的了解，预测值都会想真实值进行靠拢,而不同的G值决定了不同的靠拢速度，相同预测值与真实的情况下，G为2的学习速率将是G为1的两倍。

4. 完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
import gym
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import random
import time
from collections import deque

# Hyper Parameters for PG Network
GAMMA = 0.95  # discount factor
LR = 0.01  # learning rate

device = torch.device("cpu" if torch.cuda.is_available() else "cpu")


class PGNetwork(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(PGNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, 20)
        self.fc2 = nn.Linear(20, action_dim)

    def forward(self, x):
        out = F.relu(self.fc1(x))
        out = self.fc2(out)
        return out

    def initialize_weights(self):
        for m in self.modules():
            nn.init.normal_(m.weight.data, 0, 0.1)
            nn.init.constant_(m.bias.data, 0.01)
            # m.bias.data.zero_()


class PG(object):
    # dqn Agent
    def __init__(self, env): 
        # 状态空间和动作空间的维度
        self.state_dim = env.observation_space.shape[0]
        self.action_dim = env.action_space.n

        # 初始化状态、行为、奖励存储序列
        self.ep_obs, self.ep_as, self.ep_rs = [], [], []
        
        self.network = PGNetwork(state_dim=self.state_dim, action_dim=self.action_dim).to(device)
        self.optimizer = torch.optim.Adam(self.network.parameters(), lr=LR)
        
        self.time_step = 0

    def choose_action(self, observation):
        observation = torch.FloatTensor(observation).to(device)
        network_output = self.network.forward(observation)
        with torch.no_grad():
            prob_weights = F.softmax(network_output, dim=0).cuda(1).data.cpu().numpy()
        
        action = np.random.choice(range(prob_weights.shape[0]),
                                  p=prob_weights)  # select action w.r.t the actions prob
        return action

    # 将状态，动作，奖励这一个transition保存到三个列表中
    def store_transition(self, s, a, r):
        self.ep_obs.append(s)
        self.ep_as.append(a)
        self.ep_rs.append(r)
        
    def _discount_and_norm_rewards(self):
        """
            计算每一个G值状态计算
        """
         # Step 1: 计算每一步的状态价值
        discounted_ep_rs = np.zeros_like(self.ep_rs)
        running_add = 0
        # 注意这里是从后往前算的，所以式子还不太一样。算出每一步的状态价值
        # 前面的价值的计算可以利用后面的价值作为中间结果，简化计算；从前往后也可以
        for t in reversed(range(0, len(self.ep_rs))):
            running_add = running_add * GAMMA + self.ep_rs[t]
            discounted_ep_rs[t] = running_add

        discounted_ep_rs -= np.mean(discounted_ep_rs)  # 减均值
        discounted_ep_rs /= np.std(discounted_ep_rs)  # 除以标准差
        return discounted_ep_rs

    def learn(self):
        self.time_step += 1
        # step1：G值计算
        discounted_ep_rs = self._discount_and_norm_rewards()
        discounted_ep_rs = torch.FloatTensor(discounted_ep_rs).to(device)

        # Step 2: 前向传播
        softmax_input = self.network.forward(torch.FloatTensor(self.ep_obs).to(device))
        neg_log_prob = F.cross_entropy(input=softmax_input, target=torch.LongTensor(self.ep_as).to(device), reduction='none')    # 当前Policy Gradient网络计算出的行为与实行的行为之间的差异

        # Step 3: 反向传播
        loss = torch.mean(neg_log_prob * discounted_ep_rs)   # 根据选择的Action与实际进行的Action之间的差异与各步的奖惩分配比率计算每步的损失
        self.optimizer.zero_grad()
        loss.backward()
        self.optimizer.step()
        
        # 每次学习完后清空数组
        self.ep_obs, self.ep_as, self.ep_rs = [], [], []



# 超参数
ENV_NAME = 'CartPole-v0'
EPISODE = 3000  # Episode limitation
STEP = 300  # 一个episode最多能采取的step数
TEST = 10  # The number of experiment test every 100 episode


def main():
    # initialize OpenAI Gym env and dqn agent
    env = gym.make(ENV_NAME)
    agent = PG(env)

    for episode in range(EPISODE):
        state = env.reset()
        for step in range(STEP):
            action = agent.choose_action(state)  # softmax概率选择action
            next_state, reward, done, _ = env.step(action)
            agent.store_transition(state, action, reward)   # 新函数 存取这个transition
            state = next_state
            if done:
                # print("stick for ",step, " steps")
                agent.learn()   # 更新策略网络
                break

        # Test every 100 episodes
        if episode % 100 == 0:
            total_reward = 0
            for i in range(TEST):
                state = env.reset()
                for j in range(STEP):
                    action = agent.choose_action(state)  # direct action for test
                    state, reward, done, _ = env.step(action)
                    total_reward += reward
                    if done:
                        break
            ave_reward = total_reward/TEST
            print ('episode: ', episode, 'Evaluation Average Reward:', ave_reward)


if __name__ == '__main__':
    time_start = time.time()
    main()
    time_end = time.time()
    print('The total time is ', time_end - time_start)
参考文献