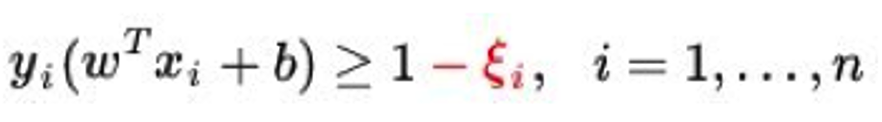SVM
什么是SVM
给定训练数据集,通过间隔最大化从策略,通过求解相应的凸二次规划问题或正则化的合页损失函数最小化问题,学习得到分离超平面为:
$$ w^x+b^=0
$$ 以及相应的分类决策函数为:
$$ f(x)=sign(w^x+b)
$$ 称为支持向量机
SVM目标是什么?
目标:找到具有最大化间隔划分的超平面
什么是函数间隔、几何间隔?有什么区别和联系?
函数间隔
对于给定的训练数据集T和超平面(w,b),定义超平面(w,b)关于样本点(xi,yi)的函数间隔为:
$$ r_i^{\^} =y_i(w·x_i+b)
$$
特点:成比例的改变w和b,超平面不会改变,但是函数间隔会成比例改变
函数间隔可以表示分类预测的正确性以及确信度,但是由于函数间隔的特点在选择分离超平面时,只有函数间隔还不够。
几何间隔
在函数间隔的基础上加入约束(||w||)使间隔不随着比例变化,这时函数间隔就转化成几何间隔。
$$ r_i=y_i(w/(||w||)·x_i+b/(||w||))
$$
超平面到样本点的几何间隔是实例点到超平面的超平面的带符号距离
二者关系
$$ r = r^/(||w||)
$$
SVM推导
SVM中为什么要把原问题转化成其对偶问题?
原问题是凸二次规划问题,转换为对偶问题更加高效。因求其对偶问题只需要求解alpha系数,而alpha系数除了支持向量(定义就是训练集中alpha>0的样本)以外全部都为0(alpha个数=训练集样本点个数)
SVM中原问题和对偶问题的关系
SVM中对偶问题中最终的解alpha和原问题的解w、b相对应,可以由KTT条件证明
什么是KTT条件?
SVM如何防止过拟合
SVM中解决过拟合最有效的方式就是在SVM的公式中引入松弛变量。目标函数中加入松弛变量的平方和
其中
为一个大小适中的值(0.2左右..),来避过一些异常点造成的过拟合,因为加入松弛变量后的异常点就不再是支持向量了,但是如果过大会失去太多本该是支持向量的点造成分类效果差,就是去了SVM的意义
SVM如何进行调参
一般当数据量不是很大时,一般使用设定一个参数的范围然后网格搜索进行调参。
核心参数:
C 模型对于误差的不宽容度,C越大说明越不能容忍误差,越容易过拟合
gamma 反应数映射到高维空间后的分布,gamma越大,支持向量越多,越容易过拟合
调参思路:
对于线性SVM,只需要调整正则化参数c的范围
rbf核的SVM,需要调节正则化参数C和核函数参数gamma
起始时二者设在0.1~10之间,每次乘以0.1或者10
两个参数要一个一个进行调节,不能两个同时进行调节